\[\sqrt{4}=\pm 2\]
\[\sqrt{0}=\pm 0\]
\[\sqrt{100}=\pm 10\]
Como se puede observar, dos números cumplen la propiedad que al multiplicarse por si mismos se obtiene el número dentro de la raíz cuadrada. Vemos entonces que la raíz cuadrada como tal no regresa un sólo valor, sino dos valores.
Para evitar la situación de que nos regrese dos valores tenemos el concepto de "raíz cuadrada principal", que es el concepto que usa la calculadora para obtener la raíz cuadrada. La "raíz cuadrada principal" de un número es el número positivo que cumple con la propiedad de la "raíz cuadrada".
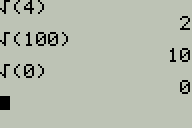 |
| La calculadora sólo regresa un resultado |
Extendamos el concepto de "raíz cuadrada" al resto de los números complejos. Los números resultantes de la raíz cuadrada serán también números complejos. Al igual que con los números reales, habrá dos raíces cuadradas para cada número negativo, para cada número imaginario y para cada número que sea una combinación de parte real y parte imaginaria. Consideremos el problema de encontrar una de las dos raíces cuadradas:
\[\textrm{Sea }z=x+yi \textrm{ . Además, sea } \sqrt{z}=u+vi\]
\[
\begin{align*}
\sqrt{z}&=\sqrt{x+yi} \\
u+vi &= \sqrt{x+yi} \\
&\textrm{Elevando al cuadrado en ambos lados}\\
(u+vi)^2&=x+yi \\
(u^2-v^2)+(2uv)i&=x+yi
\end{align*}
\]
El número del lado izquierdo es lo mismo que el número del lado derecho. Dos números complejos son iguales si su parte real y su parte imaginaria tienen el mismo valor. Por lo tanto:
\[\begin{align*}
(u^2-v^2)+(2uv)i&=x+yi \\
\textrm{Re }((u^2-v^2)+(2uv)i) &= \textrm{Re }(x+yi) \\
(u^2-v^2)&=x
\end{align*}
\]
Y también se cumple:
\[
\begin{align*}
(u^2-v^2)+(2uv)i&=x+yi \\
\textrm{Im }((u^2-v^2)+(2uv)i) &= \textrm{Im }(x+yi) \\
2uv&=y
\end{align*}
\]
Ahora usamos los resultados de las dos ecuaciones anteriores para despejar \(u\) y \(v\). Sabemos de la ecuación \(2uv=y\) que:
\[u=\frac{y}{2v}\]
\[u^2=\frac{y^2}{4v^2}\]
Lo anterior supone que la parte imaginaria no es cero, la fórmula no se cumple si la parte imaginaria sí es cero. Sustituyendo este hecho en la ecuación resultante de igualar las partes reales:
\[Lo anterior supone que la parte imaginaria no es cero, la fórmula no se cumple si la parte imaginaria sí es cero. Sustituyendo este hecho en la ecuación resultante de igualar las partes reales:
\begin{align*}
(u^2-v^2)&=x \\
\left (\left (\frac{y^2}{4v^2}\right )-v^2\right )&=x\\
\frac{y^2}{4v^2}-\frac{4v^4}{4v^2}&=x\\
\frac{y^2-4v^4}{4v^2}&=x\\
y^2-4v^4&=4xv^2\\
0&=4v^4+4xv^2+(-y^2)
\end{align*}
\]
La ecuación anterior es una ecuación cuadrática escondida. Recordemos que los valores de \(x\) y los valores de \(y\) son constantes ya dadas. Si rescribimos la expresión y sustituimos \(p=v^2\) podremos verlo más claro:
\[
\begin{align*}
0&=4(v^2)^2+(4x)(v^2)+(-y^2)\\
0&=4p^2+(4x)p+(-y^2)
\end{align*}
\]
\[
\begin{align*}
0&=4(v^2)^2+(4x)(v^2)+(-y^2)\\
0&=4p^2+(4x)p+(-y^2)
\end{align*}
\]
Entonces resolviendo esta cuadrática con la fórmula cuadrática tenemos:
\[p=\frac{(-4x)\pm \sqrt{(4x)^2-4(4)(-y^2)}}{(2)(4)}\]
\[p=\frac{(-4x)\pm \sqrt{16x^2+16y^2}}{8}\]
\[p=\frac{(-4x)\pm 4\sqrt{x^2+y^2}}{8}\]
\[p=\frac{-x\pm \sqrt{x^2+y^2}}{2}\]
\[v^2=\frac{-x\pm\sqrt{x^2+y^2}}{2}\]
\[v=\pm\sqrt{\frac{-x\pm\sqrt{x^2+y^2}}{2}}\]
\[v=\pm\sqrt{\frac{-x\pm|z|}{2}}\]
Con lo anterior vemos que \(v\) puede tomar cuatro valores posibles, ya que puede ser positivo o negativo y después la raíz cuadrada puede tomar dos valores. Sin embargo hay que ignorar los valores imaginarios, ya que establecimos que \(v\) tiene que ser un número únicamente real. Al ignorar los valores imaginarios de \(v\) terminaremos con dos posibles valores. Sabemos que \(|z|\) siempre será un número positivo o cero mayor o igual al valor de \(x\), por lo tanto debemos de eliminar el signo negativo para que se pueda obtener un número real:
\[v=\pm\sqrt{\frac{|z|-x}{2}}\]
\[v=\pm\sqrt{\frac{-x\pm\sqrt{x^2+y^2}}{2}}\]
\[v=\pm\sqrt{\frac{-x\pm|z|}{2}}\]
Con lo anterior vemos que \(v\) puede tomar cuatro valores posibles, ya que puede ser positivo o negativo y después la raíz cuadrada puede tomar dos valores. Sin embargo hay que ignorar los valores imaginarios, ya que establecimos que \(v\) tiene que ser un número únicamente real. Al ignorar los valores imaginarios de \(v\) terminaremos con dos posibles valores. Sabemos que \(|z|\) siempre será un número positivo o cero mayor o igual al valor de \(x\), por lo tanto debemos de eliminar el signo negativo para que se pueda obtener un número real:
\[v=\pm\sqrt{\frac{|z|-x}{2}}\]
En la fórmula anterior, la raíz cuadrada debe de considerarse que obtiene dos valores posibles. Una vez obtenido el valor de \(v\), una simple sustitución con \(2uv=y\) nos deja el valor de \(u\):
\[u=\pm\frac{y}{2v}\]
\[u=\pm\frac{y}{2\sqrt{\frac{|z|-x}{2}}}\]
\[u=\pm\frac{y}{2\sqrt{\frac{|z|-x}{2}}}\]
A consecuencia de que \(v\) toma dos valores posibles, tendremos dos valores correspondientes de \(u\). Lo que sucederá es que, al igual que con los números reales positivos, las raíces cuadradas de los números complejos también serán dos resultados. Como \(u\) y \(v\) comparten el \(\pm\), podemos expresar las dos posibles respuestas como \(\pm\sqrt{z}=\pm(u+vi)\). Los valores de \(u\) y \(v\) correspondientes pueden ser cualquier número real, incluso pueden tener signos opuestos.
Cabe notar que la fórmula obtenida para \(u\) y \(v\) aplica para todo número complejo que no sea real. Exceptuando el cero que sólo sí mismo es su raíz cuadrada.
Para los números reales negativos podemos utilizar la unidad imaginara para darnos cuenta de cuáles son las dos raíces cuadradas de un número negativo, sea \(a \in \mathbb{R}\) y \(a > 0\):
\[(\sqrt{a}i)(\sqrt{a}i)=(\sqrt{a})^2(i)^2 = -a\]
\[(-\sqrt{a}i)(-\sqrt{a}i)=(-1)^2(\sqrt{a})^2(i)^2 = -a\]
Por lo tanto:
\[\pm\sqrt{-a}=\pm\sqrt{-1}\sqrt{a}=\pm \sqrt{a}i \]
Veamos algunos ejemplos de las raíces cuadradas (obteniendo dos resultados) de números complejos:
\[\sqrt{1}=\pm 1\]
\[\sqrt{100}=\pm 10\]
\[\sqrt{-1}=\pm i\]
\[\sqrt{-100}=\pm 10i\]
\[\sqrt{i}=\pm \left (\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right )\]
\[\sqrt{100i}=\pm \left (\sqrt{50}+\sqrt{50}i\right )\]
\[\sqrt{-i}=\pm \left (\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i\right )\]
\[\sqrt{-100i}=\pm \left (\sqrt{50}-\sqrt{50}i\right )\]
\[\sqrt{2+3i}=\pm \left (\frac{3\sqrt{\frac{-2+\sqrt{13}}{2}}}{-2+\sqrt{13}}+\sqrt{\frac{-2+\sqrt{13}}{2}}i\right )\]
\[\sqrt{-2+3i}=\pm \left (\frac{3\sqrt{\frac{2+\sqrt{13}}{2}}}{2+\sqrt{13}}+\sqrt{\frac{2+\sqrt{13}}{2}}i\right )\]
\[\sqrt{2-3i}=\pm \left (-\frac{3\sqrt{\frac{-2+\sqrt{13}}{2}}}{-2+\sqrt{13}}+\sqrt{\frac{-2+\sqrt{13}}{2}}i\right )\]
\[\sqrt{-2-3i}=\pm \left (-\frac{3\sqrt{\frac{2+\sqrt{13}}{2}}}{2+\sqrt{13}}+\sqrt{\frac{2+\sqrt{13}}{2}}i\right )\]
La calculadora también puede regresar las raíces principales de algunas de las operaciones anteriores.
Se decidió hacer \(i\) la raíz principal de \(-1\), esta es la definición de \(i\) que algunos usan.

No hay comentarios.:
Publicar un comentario